Florian Lehner's Webpage
About me

I am a lecturer at the Department of Mathematics at the University of Auckland.
My research interests cover a wide variety of topics in graph theory and combinatorics. Much of my work concerns problems on the interface of group theory and graph theory, but I also enjoy working on topics with a geometric or probabilistic flavour.
Recent research
Asymmetric graph colouring
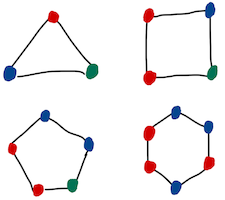 How hard is it, to get rid of the symmetries of a discrete structure? More precisely, how many colours do we need to colour the vertices of a graph in a way that no automorphism except the identity preserves the colouring?
How hard is it, to get rid of the symmetries of a discrete structure? More precisely, how many colours do we need to colour the vertices of a graph in a way that no automorphism except the identity preserves the colouring?
The least number of colours required is called the asymmetric colouring number or distinguishing number of the graph. I have studied this graph invariant in various settings, including random colourings, edge colourings, and most recently colourings of graphs with bounded maximum degree.
Combinatorial game theory
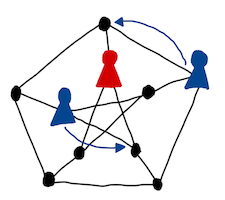 The study of pursuit-evasion games on graphs is a popular topic in combinatorial game theory. These are games where one player's objective is to capture the other player, whereas the other player attempts to avoid being captured. Notable examples include Cops-and-Robber and Conway's Angel-Devil game.
The study of pursuit-evasion games on graphs is a popular topic in combinatorial game theory. These are games where one player's objective is to capture the other player, whereas the other player attempts to avoid being captured. Notable examples include Cops-and-Robber and Conway's Angel-Devil game.
My contributions mostly concern the so-called cop number, that is, the least number of pursuers needed to guarantee capture in the Cops-and-Robber game, but I am always interested in learning about other aspects of the game as well as other combinatorial games.
Tree structure in infinite graphs
 Stallings' splitting theorem is one of the central results in geometric group theory. It essentially states that a finitely generated group satisfies one of two alternatives. It either has one well-connected infinite part (that is, it is one-ended), or it exhibits a large-scale tree structure (either an amalgamated free product, or a HNN extension).
Stallings' splitting theorem is one of the central results in geometric group theory. It essentially states that a finitely generated group satisfies one of two alternatives. It either has one well-connected infinite part (that is, it is one-ended), or it exhibits a large-scale tree structure (either an amalgamated free product, or a HNN extension).
Hamann, Miraftab, Rühmann, and I recently proved an analogous result for infinite graphs; I am currently working on applications as well as further extensions of this result.
Resume
You can also download a CV in PDF format.
Employment
| Senior Lecturer Department of Mathematics, University of Auckland | since 2025 |
| Lecturer Department of Mathematics, University of Auckland | 2022 – 2025 |
| Project Assistant Department of Discrete Mathematics, Graz University of Technology | 2020 – 2022 |
| Erwin Schrödinger Research Fellow Department of Mathematics, University of Warwick Department of Discrete Mathematics, Graz University of Technology | 2017 – 2020 |
| University Assistant (Postdoc) Department of Mathematics, University of Hamburg | 2015 – 2017 |
| University Assistant Institute of Geometry, Graz University of Technology | 2011 – 2015 |
| Teaching Assistant Mathematics Institutes and Institute for Software Technology, Graz University of Technology | 2007 – 2010 |
Education
| PhD: Mathematics and Scientific Computing Graz University of Technology Graduation with highest distinctions "Sub auspiciis Praesidentis" Thesis: Symmetry breaking in graphs and groups. Adviser: J. Wallner | 2011 – 2014 |
| Master Programme: Mathematical Computer Science Graz University of Technology Thesis: The line graph of every locally finite 6-edge-connected graph with finitely many ends is hamiltonian. Adviser: W. Woess | 2008 – 2011 |
| Bachelor Programme: Technical Mathematics Graz University of Technology | 2005 – 2008 |
Publications
Articles
| [48] | On weak cop numbers of transitive graphs. 2025, preprint. pdf |
| [47] | Hamiltonicity of transitive graphs whose automorphism group has ℤp as commutator subgroup. 2024, preprint. pdf |
| [46] | Sparse cycle bases for graphs with bounded genus. 2024, preprint. pdf |
| [45] | Locally finite graphs and their localization numbers. 2024, preprint. pdf |
| [44] | Self-avoiding walk is ballistic on graphs with more than one end. 2024, preprint. pdf |
| [43] | Folding polyominoes into cubes. 2024, preprint. pdf |
| [42] | Catching a robber on a random k-uniform hypergraph. Canadian Journal of Mathematics, 2024, to appear. pdf |
| [41] | Chromatic number is not tournament-local. Journal of Combinatorial Theory, Series B, 168, pp. 86 – 95, 2024. pdf |
| [40] | Asymmetrizing infinite trees. 2023, preprint. pdf |
| [39] | Tipsy cop and tipsy robber: collisions of biased random walks on graphs. Theoretical Computer Science, 997, 114512, 2024. pdf |
| [38] | Asymmetric colouring of locally compact permutation groups. Bulletin of the London Mathematical Society, 55(4), pp. 1874 – 1879, 2023. doi pdf |
| [37] | A note on classes of subgraphs of locally finite graphs. Journal of Combinatorial Theory, Series B, 161, pp. 52 – 62, 2023. doi pdf |
| [36] | Universal planar graphs for the topological minor relation. Combinatorica, 44, pp. 209 – 230, 2023. doi pdf |
| [35] | Self-avoiding walks and multiple context-free languages. Combinatorial Theory, 3 (1), 2023. doi pdf |
| [34] | Hamiltonian decompositions of 4-regular Cayley graphs of infinite abelian groups. Journal of Graph Theory, 101 (3), pp. 559 – 571, 2022. doi pdf |
| [33] | On fixity of arc-transitive graphs. Science China Mathematics, 64, pp. 2603 – 2610, 2021. doi pdf |
| [32] | Counterexamples to "A Conjecture on Induced Subgraphs of Cayley Graphs". Ars Mathematica Contemporanea, 19 (1), pp. 77 – 82, 2020. doi pdf |
| [31] | Comparing consecutive letter counts in multiple context-free languages. Theoretical Computer Science, 868, pp. 1 – 5, 2021. doi pdf |
| [30] | On asymmetric colourings of graphs with bounded degrees and infinite motion. Ars Mathematica Contemporanea, 2024, to appear. pdf |
| [29] | A bound for the distinguishing index of regular graphs. European Journal of Combinatorics, 89, 2020. doi pdf |
| [28] | Bounding the cop number of a graph by its genus. SIAM Journal on Discrete Mathematics, 35 (4), pp. 2459 – 2489, 2021. doi pdf |
| [27] | On the cop number of toroidal graphs. Journal of Combinatorial Theory, Series B, 151, pp. 250 – 262, 2021. doi pdf |
| [26] | A Stallings' type theorem for quasi-transitive graphs. Journal of Combinatorial Theory, Series B, 157, pp. 40 – 69, 2022. doi pdf |
| [25] | Invariant spanning double rays in amenable groups. Discrete Mathematics, 344(2), 2021. doi pdf |
| [24] | Distinguishing infinite graphs with bounded degrees. Journal of Graph Theory, 101(1), pp. 52 – 65, 2022. doi pdf |
| [23] | Distinguishing numbers of finite 4-valent vertex-transitive graphs. Ars Mathematica Contemporanea, 19 (2), pp. 173 – 187, 2020. doi pdf |
| [22] | On symmetries of edge and vertex colourings of graphs. Discrete Mathematics, 343 (9), 2020. doi pdf |
| [21] | Distinguishing density and the Distinct Spheres Condition. European Journal of Combinatorics, 89, 2020. doi pdf |
| [20] | Hamilton decompositions of one-ended Cayley graphs. Journal of Combinatorial Theory, Series B, 140, pp. 171 – 191, 2020. doi pdf |
| [19] | Trees with distinguishing index equal distinguishing number plus one. Discussiones Mathematicae Graph Theory, 40 (3), pp. 875 – 884, 2020. doi pdf |
| [18] | Firefighting on trees and Cayley graphs. Australasian Journal of Combinatorics, 75 (1), pp. 66 – 72, 2019. jrnl pdf |
| [17] | On tree-decompositions of one-ended graphs. Mathematische Nachrichten, 292 (3), pp. 524 – 539, 2018. doi pdf |
| [16] | A counterexample to Montgomery's conjecture on dynamic colourings of regular graphs. Discrete Applied Mathematics, 229, pp. 151 – 153, 2017. doi pdf |
| [15] | Non-reconstructible locally finite graphs. Journal of Combinatorial Theory, Series B, 133, pp. 122 – 152, 2018. doi pdf |
| [14] | A counterexample to the reconstruction conjecture for locally finite trees. Bulletin of the London Mathematical Society, 49 (4), pp. 630 – 648, 2017. doi pdf |
| [13] | Breaking graph symmetries by edge colourings. Journal of Combinatorial Theory, Series B, 127, pp. 205 – 214, 2017. doi pdf |
| [12] | Fast factorization of Cartesian products of (directed) hypergraphs. Theoretical Computer Science, 615, pp. 1 – 11, 2016. doi pdf |
| [11] | Maximising the number of independent sets in connected graphs. Graphs and Combinatorics, 33 (5), pp. 1103 – 1118, 2017. doi pdf |
| [10] | Local finiteness, distinguishing numbers and Tucker's conjecture. Electronic Journal of Combinatorics, 22 (4), 2015, research paper #P4.19. doi pdf |
| [9] | Pursuit evasion on infinite graphs. Theoretical Computer Science, 655 (Part A), pp. 30 – 40, 2016. doi pdf |
| [8] | The Cartesian product of graphs with loops. Ars Mathematica Contemporanea, 11 (1), pp. 1 – 9, 2016. doi pdf |
| [7] | Clique trees of infinite locally finite chordal graphs. Electronic Journal of Combinatorics, 25 (2), 2018, research paper #P2.9. doi pdf |
| [6] | Extending cycles locally to Hamilton cycles. Electronic Journal of Combinatorics, 23 (1), 2016, research paper #P1.49. doi pdf |
| [5] | Random colorings and automorphism breaking in locally finite graphs Combinatorics, Probability and Computing, 22 (6), pp. 885 – 909, 2013. doi pdf |
| [4] | Distinguishing graphs with intermediate growth. Combinatorica, 36 (3), pp. 333 – 347, 2016. doi pdf |
| [3] | Endomorphism breaking in graphs. Electronic Journal of Combinatorics, 21 (1), 2014, research paper #P1.16. doi pdf |
| [2] | Distinguishing graphs with infinite motion and nonlinear growth. Ars Mathematica Contemporanea, 7, pp. 201 – 213, 2014. doi pdf |
| [1] | On spanning tree packings of highly edge connected graphs. Journal of Combinatorial Theory, Series B, 105, pp. 93 – 126, 2014. doi pdf |
Theses
| [2] | Symmetry breaking in graphs and groups Ph.D. Thesis, TU Graz, 2014. pdf |
| [1] | The line graph of every locally finite 6-edge-connected graph with finitely many ends is hamiltonian. Master thesis, TU Graz, 2011. pdf |